https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
인덱스 트리를 구현하는 문제이다.
인덱스 트리의 method는 init, query, update가 있으며, bottom-up, top-down으로 모두 구현할 수 있다. 개념자체는 어렵지 않다.
Bottom-up으로 풀리지 않는 문제를 Top-down으로 풀 수 있기 때문에 두가지 approach를 모두 익힐 시간이 없다면 top-down이라도 연습하는 것이 좋다.

인덱스 트리는 위의 그림처럼 생겼다. leaf node에는 입력받은 데이터가 들어있고, 부모 노드에는 각 자식 노드들의 합을 기록한다.
인덱스 트리는 부분합을 구하기 쉬울 뿐더러 data값이 변경된다면 인덱스 트리를 사용하는 것이 효율적이다.
Top-down
말 그대로 위에서부터 채워 나가는 방식이다. 배열을 초기화하기 위해서 크기가 필요한데, 이 때 leaf node의 수가 실제 데이터의 크기와 같거나 보다 큰 2의 제곱수(=S)가 되어야하므로 크기를 2*S+1로 초기화한다.
init ( int left, int right, int node )
node는 현재 인덱스를 말하고, left와 right는 위 그림에 써있는 index를 나타낸다.
top-down은 root에서 시작하니 left는 1, right는 8, node는 1로 시작한다.
현재 노드가
- leaf 노드라면 데이터를 트리에 저장
- 내부 노드라면 왼쪽 자식, 오른쪽 자식으로 각각 init 호출 후, 왼쪽 자식과 오른쪽 자식의 value를 합쳐 저장한다.
query ( int left, int right, int node, int queryLeft, int queryRight )
여기서 query method는 queryLeft와 queryRight사이의 값의 합을 return한다.
따라서 query( 1, 8, 1, 3, 7 ) 을 호출하면 데이터의 3번부터 7번까지의 합을 return 해준다.

그럼 녹색으로 칠한 부분의 값의 합을 return 하면 효율적으로 query를 수행할 수 있다.
어느 노드의 값을 return할 지는 현재 left, right값과 queryLeft, queryRight의 범위를 비교하여 판단한다.

1-8 에서 판단이 불가능하기 때문에 자식에게 넘긴다.
1-4, 5-8에서도 판단이 불가능하기 때문에 자식에게 넘긴다.
1-2에서는 연관이 없기 때문에 0을 return하고
3-4, 5-6 에서는 판단 가능하기 때문에 해당 node의 value를 return한다.
7-8 에서는 판단 불가능하기 때문에 자식에게 넘기고
7은 판단 가능, 8은 연관없음이다.
update ( int left, int right, int node, int target, int diff )
target은 변경할 노드의 인덱스이고, diff는 변경전과 후 value의 차이다. diff값을 더해 값을 변경한다고 하면 3번 노드를 5에서 7로 변경할 때 diff값은 2이다.
target이 left와 right 사이에 있다면 해당 노드의 값을 변경하면서 target까지 들어간다.
연관 없다면 return한다.
Bottom-up
Bottom-up은 말그대로 아래에서부터 올라온다. Bottom-up 방식에서 특히 S(데이터 사이즈와 같거나 보다 큰 2의 제곱수) 라는 개념이 중요하다.
init()
leaf 노드를 가장 먼저 순회하고 난 후에 내부노드로 올라와 S-1부터 1까지 순회한다. 순회 순서는 아래와 같다.
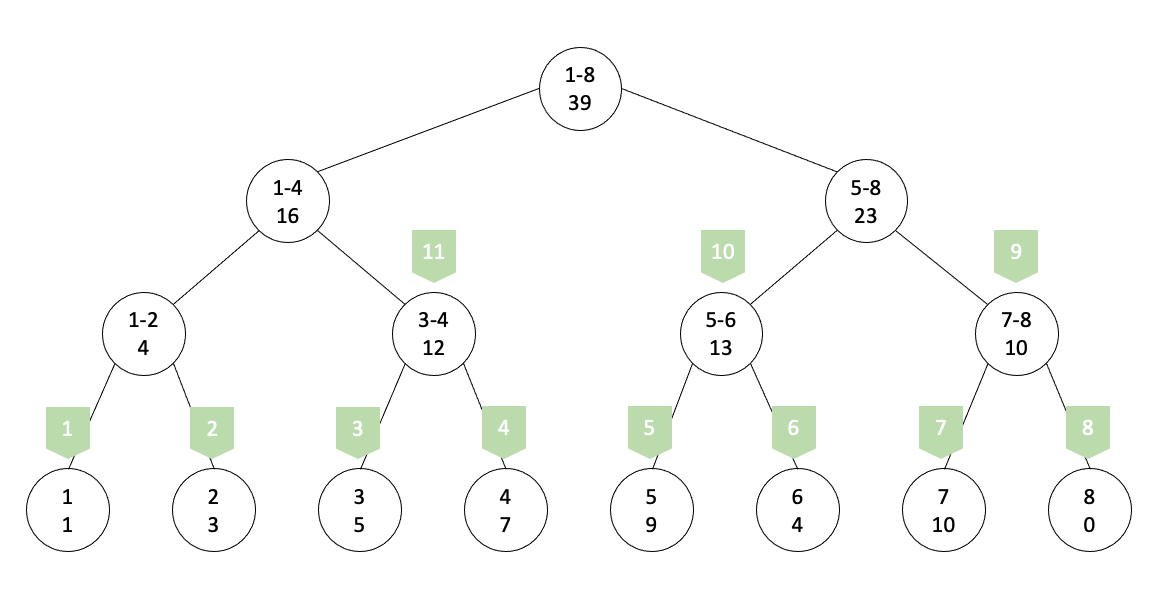
tree에서 leaf노드의 index는 node+S-1이다.
예를 들어 3번 노드의 index는 3+S-1 = 10이다.
query ( int queryLeft, int queryRight )
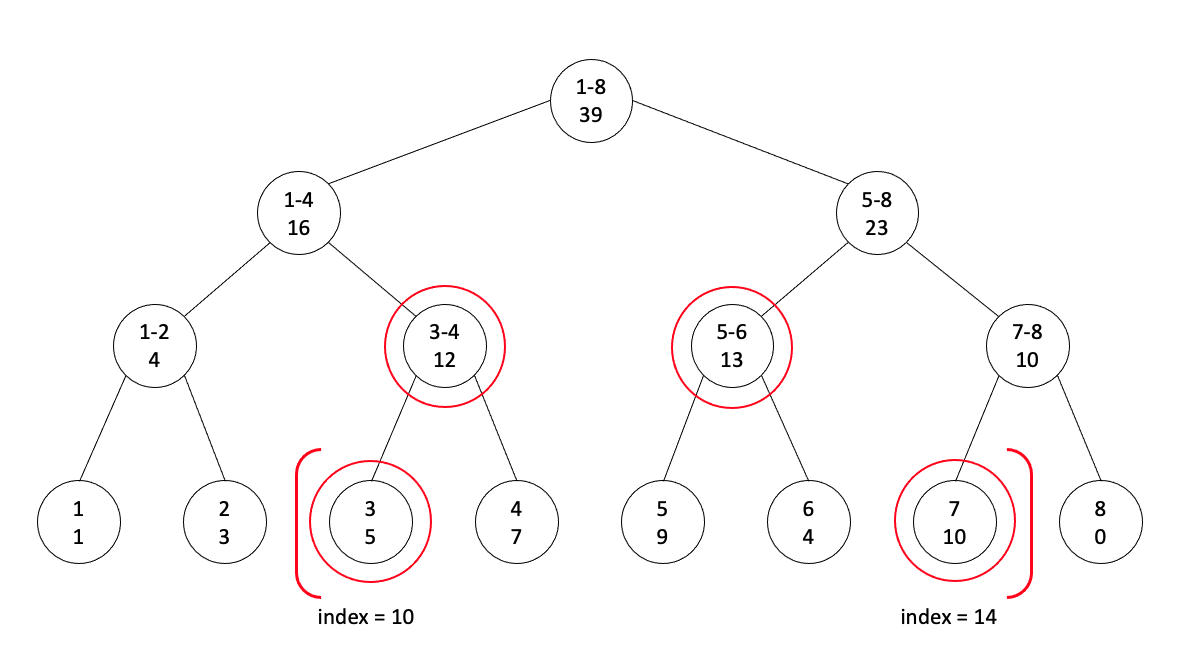
left의 tree index가 짝수 : 부모의 값 사용, left = left / 2
left의 tree index가 홀수 : 자신의 값을 사용, left = ( left + 1 ) / 2
right의 tree index가 짝수 : 자신의 값을 사용, right = ( right - 1 ) / 2
right의 tree index가 홀수 : 부모의 값 사용, right = right / 2
update ( int target, int value )
target은 바꿀 노드, value는 차가 아니라 바꿀 값이다. target노드에서 해당 값으로 변경하고 부모로 이동한다.
부모는 자식 둘의 합으로 update한다. root 노드까지 진행한다.
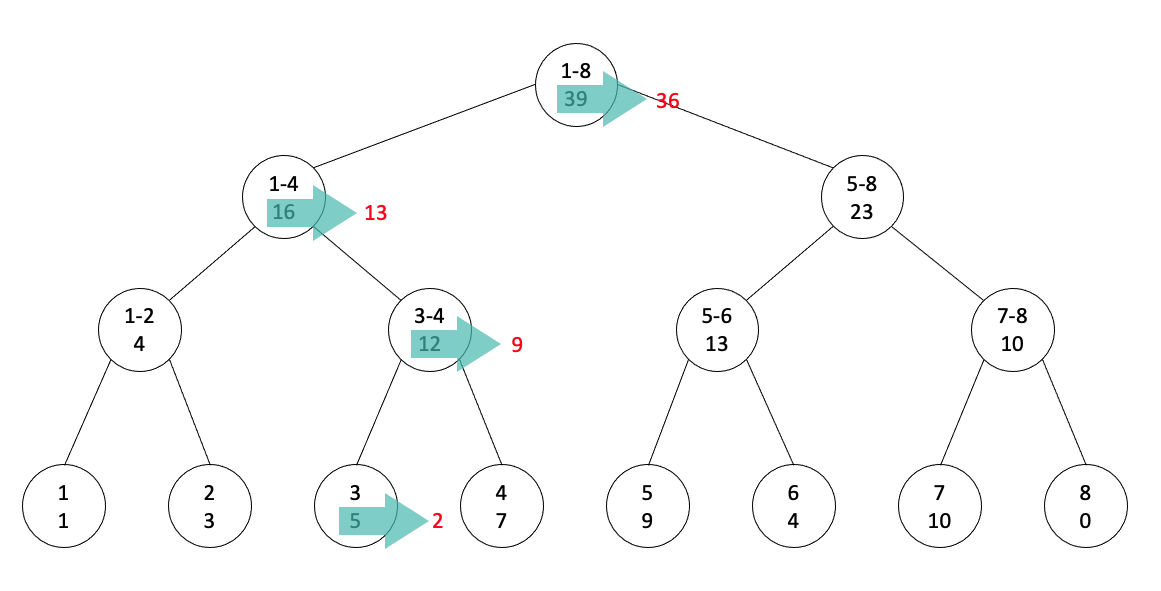
풀이는 top-down으로 했다.
// 2042 풀이
public class Main {
static long[] data;
static long[] tree;
static long S;
public static void main(String[] args) throws Exception {
//System.setIn(new FileInputStream("src/P2042/input.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
data = new long[N];
for(int i=0; i<N; i++) data[i] = Long.parseLong(br.readLine());
S = 1;
while(S<=N) S*=2;
tree = new long[(int)(2*S+1)];
init(1, (int)S, 1);
for(int i=0; i<M+K; i++){
st = new StringTokenizer(br.readLine());
long a = Long.parseLong(st.nextToken());
long b = Long.parseLong(st.nextToken());
long c = Long.parseLong(st.nextToken());
if(a==1){
long diff = c-tree[(int)(b+S-1)];
update(1, (int)S, 1, (int)b, diff);
}
else if(a==2){
long res = query(1, (int)S, 1, (int)b, (int)c);
System.out.println(res);
}
}
}
static void init(int left, int right, int node){
// leaf 노드라면 데이터 저장
if(left==right && (node-S)<data.length) tree[node] = data[(int)(node-S)];
// 내부노드라면 자식의 합 저장
else if(left<right){
int mid = (left+right)/2;
init(left, mid, node*2);
init(mid+1, right, (node*2)+1);
tree[node] = tree[2*node] + tree[2*node+1];
}
}
static long query(int left, int right, int node, int queryLeft, int queryRight){
// 관련 없는 구간이라면 0 리턴
if(queryLeft > right || queryRight < left) return 0;
// 판단 가능한 구간
else if( queryLeft <= left && right <= queryRight){
return tree[node];
}
// 판단이 불가능해서 자식에게 넘기는 구간
else {
int mid = (left+right)/2;
long leftRes = query(left, mid, node*2, queryLeft, queryRight);
long rightRes = query(mid+1, right, 2*node+1, queryLeft, queryRight);
return leftRes+rightRes;
}
}
static void update(int left, int right, int node, int target, long diff){
// 연관 없음
if(target < left || target > right) return;
// 연관 있음
else {
tree[node] += diff;
if(left!=right) {
int mid = (left+right)/2;
update(left, mid, 2*node, target, diff);
update(mid+1, right, 2*node+1, target, diff);
}
}
}
}'알고리즘' 카테고리의 다른 글
| [백준 - 1644] 소수의 연속합 - Java (0) | 2022.02.09 |
|---|---|
| [백준 - 2243] 사탕상자 - Java (0) | 2022.02.08 |
| [백준 - 1202] 보석 도둑 - Java (0) | 2022.02.07 |
| [백준 - 2096] 내려가기 - Java (0) | 2022.02.07 |
| [백준 - 1806] 부분합 - Java (0) | 2022.02.07 |


